Classifying Pokemon Competitively¶
Introduction¶
Pokemon is one of the most popular gaming franchises in existence, and for good reason. It features an engrossing combat system, where Pokemon battle against each other in turn based combat until one team is out of usable Pokemon.
As a result of its popularity as well as strategic nature, Pokemon has a well established competitive scene. A well known site, Smogon, is the hub of the competitive scene, and it classifies all Pokemon into separate "tiers", ranging from Ubers, for the most powerful Pokemon in the game, to Little Cup (LC), designed for even the weakest of baby Pokemon.
Most of these tiers are based on usage in competitive play - Pokemon who are used less are ranked lower. While this isn't exactly a measurement of a Pokemon's competitive strength, Pokemon which are used less frequently are nearly always weaker or at least more niche, as otherwise those Pokemon would be used more.
So what exactly determine's a Pokemon's competitive viability? This essentially boils down to five factors:
- base stats
- type
- ability
- movepool
If you're already familiar with these terms, feel free to skip the next section.
Base stats¶
Each Pokemon is given a set of base stats, which determines the actual numeric value of a Pokemon's, well, stats.
Each Pokemon has six stats:
- HP: This is the amount of health a Pokemon has. When the HP reaches 0, the Pokemon faints and is unable to battle.
- Attack: This is the physical attack stat a Pokemon has. In Pokemon, moves either do "physical" or "special" damage, and this stat determines how much damage "physical" attacks will do to other Pokemon.
- Defense: This is the physical defense, which determines how much damage physical attacks will inflict on the Pokemon.
- Special Attack: This is the special counterpart to Attack. It indicates how much damage a special attack the Pokemon will do to others.
- Special Defense: This is the special counterpart to Defense. It indicates how much damage special attacks will inflict on the Pokemon.
- Speed: Speed determines which Pokemon goes first in a turn.
Clearly, stats play a very direct role in determining the strength of a Pokemon - it determines how much damage it can take as well as how much damage it can deal.
Type¶
Each Pokemon has either one or two types. These types determine the effectiveness of moves on the Pokemon. For example, fire type Pokemon take supereffective (2x) damage from water type moves.
Furthermore, the type of a Pokemon also affects the offensive capabilities through a mechanic called "Same Type Attack Bonus" (STAB). STAB makes it so that if a Pokemon uses a move of the same type as the Pokemon, it will deal 1.5x damage. For example, if an ice type Pokemon uses an ice type move, it will deal 1.5x damage than if it had used a move of a different type.
Since different types have different strengths and weaknesses, the typing of a Pokemon greatly affects its viability.
Ability¶
Each Pokemon also has an ability, which essentially provides some sort of special bonus in combat. A simple ability is one such as "Blaze", which increases the damage of fire type moves when the Pokemon has low HP. There are more complicated abilities, such as "Drizzle", which changes the weather, which causes a variety of effects in battle.
These abilities can range from game-changingly strong to cripplingly weak, and can determine the viability of a Pokemon all by itself.
Movepool¶
Each Pokemon has a set of moves it can learn. Naturally, this directly affects the viability of a Pokemon - if a Pokemon only learns weak moves, it's going to be weaker than if it learned stronger moves.
These factors will be the inputs to our classifier.
Tiers¶
All these things determine the tier of the Pokemon. These tiers are, in descending order of viability:
- Anything Goes (AG): A tier solely for Mega-Rayquaza, as it was too powerful for even the Uber tier.
- Uber: These are Pokemon are too powerful for normal competitive play. Ubers is essentially a banlist for Pokemon that are simply too strong.
- Overused (OU): These are the strongest Pokemon in the competitive metagame.
- Underused (UU): These are strong Pokemon, but weaker than those on OU.
- Rarelyused (RU)
- Neverused (NU)
- PU (not an acronym)
- Untiered: These Pokemon are too weak to be considered viable in any of the above tiers.
- Not fully evolved (NFE): These are Pokmeon that are not fully evolved (the Pokemon is not in it's final form).
- Little Cup (LC): These Pokemon are the first evolution in its line.
Strictly speaking, NFE and LC are not really a "tier" but rather a separate entity on their own. However, when talking about viability, they are both generally worse than "Untiered" Pokemon.
There are also tiers in between the tiers, denoted as borderline tiers (though "BL" actually stands for "banlist"). For example, "UUBL" denotes the tier for Pokemon too weak to truly be in OU, but too strong for the UU metagame.
Purpose¶
Real world use¶
Okay, so suppose we make this classifier. What's the point?
One issue with competitive play is that it takes a while for a metagame to settle. That is, when new Pokemon are introduced, it takes a while for the metagame to adapt to the presence of a new Pokemon. For example, Game Freak just released addition content for Pokemon Sword and Shield, called the "Isle of Armor", which introduced many new Pokemon into the game, resulting in the competitive scene to be fairly unstable.
A tool such as this would assist in expediting this adjustment period. Using this tool, one would be able to determine the relative strength of a new Pokemon will relative ease, resulting in a more stable competitive scene and a healthier metagame overall.
Data science use¶
Okay, but what's the point of the classifier in relation to the field of data science?
The main purpose here is to simply show how to perform data analysis on a dataset (this is a tutorial, after all). The goal is to introduce people who have not had experience in data science before to data science, and to show what we can do and how it works.
Part 1: Data Collection¶
As with all things involving data science, we first need, well, data!
A quick search on the internet yields this, which provides a convenient CSV file of Pokemon names, types, stats, and more.
However, this data lacks a lot of information that is typically considered when determining how strong a Pokemon is competitively. It's missing abilities, movesets, and, most of all, it doesn't actually give an indication of what tier each Pokemon is!
Unfortunately, this seems to be the only dataset that is widely circulated on the internet. So, it's up to us to construct our own dataset.
Scraping Smogon¶
When considering where to get our data, we should look towards which aspect of our data is the least common. In this case, it's quite clearly the tier of a given Pokemon, as it's not even an official aspect of the game, but rather a fan-made tiering. As a result, we should look at where the Pokemon are ranked - Smogon itself.
Conveniently, Smogon has a Pokedex page which provides us with each Pokemon's ability and tier, and if we click on the link for each Pokemon, we even get a list of viable moves.
For now, let's ignore the movepool, and simply scrape the other data. The below code does exactly that:
import numpy as np
import pandas as pd
import requests
import bs4
import json
from sklearn.decomposition import PCA
from sklearn import preprocessing
from sklearn import svm
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
from sklearn import linear_model
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import BaggingClassifier
r = requests.get("https://www.smogon.com/dex/sm/pokemon/")
dex = bs4.BeautifulSoup(r.text).find("script").prettify()[47:-11]
parsed_dex = json.loads(dex)['injectRpcs'][1][1]
pokemon = [x for x in parsed_dex['pokemon'] if x['isNonstandard'] == "Standard"]
The above code is simple - all it does is read the HTML and load the list of Pokemon into parsed_dex.
Part 2: Cleaning the Data¶
Before we can train our classifier, we have to make our data more understandable for classifiers. As the data is right now, most of it is qualitative and as a result relatively hard to understand, which could result in poor performance of our model.
Tier data¶
Looking at the data, there are actually some entries that don't have a "tier" - not even "untiered"! At a further glance, we see that these Pokemon tend to be LC-type Pokemon - first form evolutions such as Aipom and Cutiefly. However, these Pokemon were deemed too strong for the LC metagame, and were banned, resulting in them not having a tier. This means they're in a sort of "LCBL" tier, below NFE yet above LC, which is what we'll classify them as in this case.
The below code edits our data to set these Pokemon as "LCBL" tier. It also converts the "formats" list, which contains the tier data, to a single string element as the "tier" category.
for p in pokemon:
if len(p['formats']) == 0:
p['formats'].append("LCBL")
for p in pokemon:
p['tier'] = p['formats'][0]
Another thing about our tier data is that it is ordered. That is, we know that Pokemon in OU are stronger than those in UU, and Pokemon in UU are stronger than those in RU, and so on. Leaving these tiers as strings prevents a classifier from knowing this, so we change our tier data to a numeric form to let our classifier know the order.
This is known as ordinal encoding, a technique where we convert ordered qualitative data into quantitative data. The below code adds a field to our data, tier_numeric, which represents the tier, but in number form.
tiers = ["LC", "LCBL", "NFE", "Untiered", "PU", "PUBL", "NU", "NUBL", "RU", "RUBL", "UU", "UUBL", "OU", "Uber", "AG"]
tiers_nobl = ["LC", "NFE", "Untiered", "PU", "NU", "RU", "UU", "OU", "Uber"]
for p in pokemon:
p['tier_numeric'] = tiers.index(p['tier'])
Typing¶
Similarly, we perform ordinal encoding on our types - we'll have two columns, and if a Pokemon only has one type, the second column will be 0.
types = ["Normal", "Fighting", "Flying", "Poison", "Ground", "Rock", "Bug", "Ghost", "Steel", "Fire", "Water", "Grass", "Electric", "Psychic", "Ice", "Dragon", "Dark", "Fairy"]
for p in pokemon:
p['type1'] = float(types.index(p['types'][0])+1)/(len(types)+1)
p['type2'] = float(types.index(p['types'][1])+1)/(len(types)+1) if len(p['types']) > 1 else 0
Abilities¶
Similarly, we'll encode the abilities of a Pokemon the same way. Each Pokemon can have up to 3 abilities, and if it has less, the columns will be 0.
abilities = []
# first, get a list of all abilities
for p in pokemon:
for a in p['abilities']:
if a not in abilities:
abilities.append(a)
for p in pokemon:
p['ability1'] = abilities.index(p['abilities'][0])+1
p['ability2'] = abilities.index(p['abilities'][1])+1 if len(p['abilities']) > 1 else 0
p['ability3'] = abilities.index(p['abilities'][2])+1 if len(p['abilities']) > 2 else 0
Movepool¶
Movepool is a lot more complicated than the others, so for now let's ignore it. It's not in our data anyways, we'd need to scrape some more.
Part 3: Training the classifier¶
Choosing a model¶
So, we've cleaned up all our data to be a form that's easily understood by a classifier. But which model do we use?
Thankfully, scikit-learn has a very useful guide on their website: 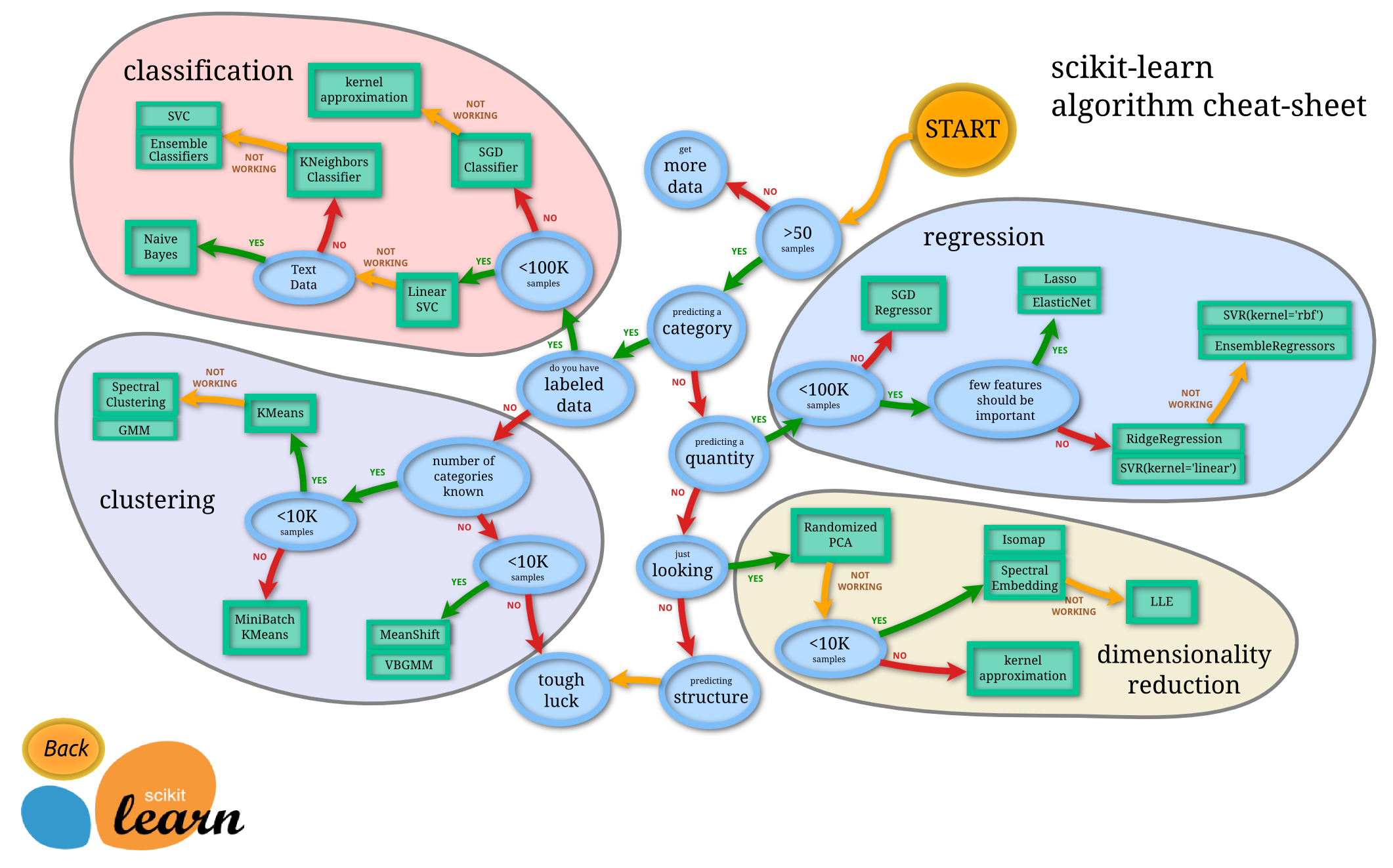
We have labelled data, and want to predict a category, which leads us to use a linear SVC. Fortunately, it's relatively simple to train a classifier with sklearn.
In the code below, we first convert our data from a dictionary to a pandas dataframe so that it is compatible with sklearn, and them we normalize the data. This prevents some columns (e.g. stats, which can reach over 100) from being valued more than others (e.g. type, which is always below 20). Then, we train a linear SVC classifier on our data, and see how it does using cross validation.
def to_df(toadd, pokemon):
df = pd.DataFrame()
for a in toadd:
df[a] = [p[a] for p in pokemon]
scaler = preprocessing.MinMaxScaler()
data_scaled = scaler.fit_transform(df.values)
df_scaled = pd.DataFrame(data_scaled, columns=df.columns)
return df_scaled
def test_clf(toadd, pokemon, ycol):
X = to_df(toadd, pokemon)
y = np.array([p[ycol] for p in pokemon])
classifier = svm.LinearSVC()
scores = cross_val_score(classifier, X, y, cv=10)
return scores
# first, convert to dataframe
stats_toadd = ['hp', 'atk', 'def', 'spa', 'spd', 'spe']
types_toadd = ['type1', 'type2']
abilities_toadd = ['ability1', 'ability2', 'ability3']
keys = stats_toadd + types_toadd + abilities_toadd
results = test_clf(keys, pokemon, 'tier_numeric')
print(np.mean(results))
Okay, so our classifier isn't doing great - it averages around 50% accuracy. Let's take a look into what sort of cases it's missing.
def view_incorrect(toadd, yvals, ycol):
X = to_df(toadd, pokemon)
y = np.array([p[ycol] for p in pokemon])
X_train, X_test, y_train, y_test = train_test_split(X, y)
clf = svm.LinearSVC()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
for c in range(len(y_test)):
if y_pred[c] != y_test[c]:
print("{}: Expected {} but got {} for pokemon {}".format("Too high" if y_test[c] < y_pred[c] else "Too low", yvals[y_test[c]], yvals[y_pred[c]], pokemon[X_test.iloc[c].name]['name']))
keys = stats_toadd + types_toadd + abilities_toadd
view_incorrect(keys, tiers, 'tier_numeric')
Looking at our results, it seems that our classifier is often classifying Pokemon into adjacent tiers (e.g. a PU Pokemon as NU or an Untiered Pokemon as PU). It's getting close, but isn't quite there. Perhaps the cardinality of our tier label is too high. Our data set is relatively small (roughly 1000 entries), so it's likely that we simply don't have enough data to deal with an output of such high cardinality. Let's try lowering it and see what happens.
tiers_comp = ["LC+NFE", "Untiered+PU+NU+RU", "UU+OU+Uber+AG"]
keys = stats_toadd + types_toadd + abilities_toadd
for p in pokemon:
for t in tiers_comp:
if p['tier'].replace("BL", '') in t:
p['tier_numeric_coarse'] = tiers_comp.index(t)
results = test_clf(keys, pokemon, "tier_numeric_coarse")
print(np.mean(results))
As expected, our accuracy drastically increases when we reduce the cardinality of tiers, reaching an average of around 70%. This is unfortunately still quite low. Furthermore, we haven't really improved anything, we're simply making the problem easier for the classifier.
Again, let's see what cases we're missing.
view_incorrect(keys, tiers_comp, 'tier_numeric_coarse')
Part 4: Improving our classifier¶
Looking at our results, it seems like our classifier fails to consider typing properly. For example, it overestimates Regice, a defensive Pokemon with great stats, but horrendous typing for a defensive Pokemon (ice).
It also, as one might predict, putting too much emphasis on base stats. For example, Archeops has great stats, but has a horrendous ability in the form of Defeatist. The classifier thinks Archeops is high tier when it is mid tier.
Furthermore, it doesn't consider movepool. The classifier underestimates Linoone, which has access to the phenomenal combination of Belly Drum and Extremespeed. Of course, we don't actually have any inputs related to movepool, so this part makes sense.
Even more concerningly is how the classifier mysteriously fails on seemingly obvious cases. For example, Kommo-o has a base stat total of 600 (very high), and yet is underestimated!
Evolutions¶
One very important feature that is not in our data is whether or not a Pokemon is fully evolved. This will be very useful in telling the classifier what tier a Pokemon is in, as unevolved Pokemon are almost always worse than their evolved counterparts.
Let's add this and see what happens:
for p in pokemon:
# add flag for fully evolved
if p['oob'] == None:
p['fully_evolved'] = 1
else:
p['fully_evolved'] = 1 if len(p['oob']['evos']) == 0 else 0
keys = stats_toadd + types_toadd + abilities_toadd + ['fully_evolved']
results = test_clf(keys, pokemon, "tier_numeric_coarse")
print(np.mean(results))
Wow! Just like that, we've improved our accuracy by around 8%! This is a great example of how simply adding another data point as part of our data can significantly affect how well our classifier does.
Typing¶
As mentioned above, one problem is that the classifier doesn't really use typing properly. This is because we encoded the type ordinally, that is, on a scale from 0 to number of types - 1. However, this implies a relationship between types that doesn't really exist. For example, "Normal" translates into 0, while Fighting translates into 1. The way we've encoded it, this implies that Fighting > Normal. It also implies that Fighting + Normal = Fighting, which is also not true. Notice that abilities have the same issue, so we'll remove them from our input data for now.
So how to we encode the type numerically without introducing this kind of false relationship?
One option is one hot encoding. That is, instead of encoding type as two columns (since Pokemon can have two types), we encode it as n columns, where each column is a boolean column that simply denotes if a Pokemon is that type.
For example, a Pokemon that is Grass/Poison will have a 1 in the columns for Grass and Poison, and 0 in all the other type columns.
This way, we prevent introducing a false relationship between types. Let's try it out and see if our classifier does any better.
types = ["Normal", "Fighting", "Flying", "Poison", "Ground", "Rock", "Bug", "Ghost", "Steel", "Fire", "Water", "Grass", "Electric", "Psychic", "Ice", "Dragon", "Dark", "Fairy"]
for p in pokemon:
for t in types:
p[t] = t in p['types']
keys = types + stats_toadd + ['fully_evolved']
results = test_clf(keys, pokemon, 'tier_numeric_coarse')
print(np.mean(results))
Okay, so adding this improved our accuracy by around 2%, which is... okay. Perhaps the classifier still isn't really learning about how typing works.
So let's think: how exactly does typing affect a Pokemon's viability?
It ultimately boils down to two factors: resistances/weaknesses and STAB.
Clearly, the more resistances a Pokemon has the better, and the more types their STAB attacks hit effectively the better. Similarly, more weaknesses is obviously worse, and inferior coverage in their STAB attacks is also worse.
Let's try adding the number of weaknesses/resistances and STAB coverage as columns. Specifically, we'll have a column each for:
- number of resistances
- number of weaknesses
- number of type combinations that are hit supereffectively by STAB moves
- number of type combinations that resist STAB moves# typing
# "Normal", "Fighting", "Flying", "Poison", "Ground", "Rock", "Bug", "Ghost", "Steel", "Fire", "Water", "Grass", "Electric", "Psychic", "Ice", "Dragon", "Dark", "Fairy"
# table of defenses - row is offensive type, col is defending type
# multiplier (0 for immune, 0.5 for resist, 1 for neutral, 2 for super)
table = [
[1, 1, 1, 1, 1, 0.5, 1, 0, 0.5, 1, 1, 1, 1, 1, 1, 1, 1, 1], # normal
[2, 1, 0.5, 0.5, 1, 2, 0.5, 0, 2, 1, 1, 1, 1, 0.5, 2, 1, 2, 0.5], # fighting
[1, 2, 1, 1, 1, 0.5, 2, 1, 0.5, 1, 1, 2, 0.5, 1, 1, 1, 1, 1], # flying
[1, 1, 1, 0.5, 0.5, 0.5, 1, 0.5, 0, 1, 1, 2, 1, 1, 1, 1, 1, 2], # poison
[1, 1, 0, 2, 1, 2, 0.5, 1, 2, 2, 1, 0.5, 2, 1, 1, 1, 1, 1], # ground
[1, 0.5, 2, 1, 0.5, 1, 2, 1, 0.5, 2, 1, 1, 1, 1, 2, 1, 1, 1], # rock
[1, 0.5, 0.5, 0.5, 1, 1, 1, 0.5, 0.5, 0.5, 1, 2, 1, 2, 1, 1, 2, 0.5], # bug
[0, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 2, 1, 1, 0.5, 1], # ghost
[1, 1, 1, 1, 1, 2, 1, 1, 0.5, 0.5, 0.5, 1, 0.5, 1, 2, 1, 1, 2], # steel
[1, 1, 1, 1, 1, 0.5, 2, 1, 2, 0.5, 0.5, 2, 1, 1, 2, 0.5, 1, 1], # fire
[1, 1, 1, 1, 2, 2, 1, 1, 1, 2, 0.5, 0.5, 1, 1, 1, 0.5, 1, 1], # water
[1, 1, 0.5, 0.5, 2, 2, 0.5, 1, 0.5, 0.5, 2, 0.5, 1, 1, 1, 0.5, 1, 1], # grass
[1, 1, 2, 1, 0, 1, 1, 1, 1, 1, 2, 0.5, 0.5, 1, 1, 0.5, 1, 1], # electric
[1, 2, 1, 2, 1, 1, 1, 1, 0.5, 1, 1, 1, 1, 0.5, 1, 1, 0, 1], # psychic
[1, 1, 2, 1, 2, 1, 1, 1, 0.5, 0.5, 0.5, 2, 1, 1, 0.5, 2, 1, 1], # ice
[1, 1, 1, 1, 1, 1, 1, 1, 0.5, 1, 1, 1, 1, 1, 1, 2, 1, 0], # dragon
[1, 0.5, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 2, 1, 0.5, 0.5], # dark
[1, 2, 1, 0.5, 1, 1, 1, 1, 0.5, 0.5, 1, 1, 1, 1, 1, 2, 2, 1] # fairy
]
for p in pokemon:
res = 0
weak = 0
# resistances/weaknesses
for t in types:
if len(p['types']) == 1:
mult = table[types.index(t)][types.index(p['types'][0])]
else:
mult = table[types.index(t)][types.index(p['types'][0])]*table[types.index(t)][types.index(p['types'][1])]
if mult < 1:
res += 1
elif mult > 1:
weak += 1
p['resistances'] = res
p['weaknesses'] = weak
# stab coverage
c1 = 0
sups = 0
nves = 0
for c1 in range(len(types)):
for c2 in range(c1+1, len(types)):
mult = 0
for t in p['types']: # only choose max multiplier
i = types.index(t)
mult = max(table[i][c1]*table[i][c2], mult)
if mult > 1:
sups += 1
elif mult < 1:
nves += 1
for c in range(len(types)):
mult = 0
for t in p['types']:
i = types.index(t)
mult = max(table[i][c], mult)
if mult > 1:
sups += 1
elif mult < 1:
nves += 1
p['stab_sups'] = sups
p['stab_nves'] = nves
new_types_toadd = ['resistances', 'weaknesses', 'stab_sups', 'stab_nves']
keys = types + stats_toadd + ['fully_evolved'] + new_types_toadd
results = test_clf(keys, pokemon, "tier_numeric_coarse")
print(np.mean(results))
...huh? Our accuracy actually went down once we added these columns! Why?
This problem is actually a result of a phenomenon called the curse of dimensionality. The curse of dimensionality occurs when your dataset has too many dimensions (columns) and not enough data (rows). We've added 22 columns just by dealing with typing! The result is that we don't have enough data for the classifier to really learn about every dimension.
This is one of the main flaws of one hot encoding - for variables with relatively high cardinality, it adds too many dimensions, resulting in lower accuracy.
Fortunately, theres a method called principal component analysis, or PCA, which extracts the most significant features out of a matrix, letting us reduce dimensionality without sacrificing much accuracy. Let's try it on our data and see what happens.
keys = types + abilities_toadd + stats_toadd + ['fully_evolved'] + new_types_toadd
df = to_df(keys, pokemon)
pca = PCA()
pca.fit(df)
print(pca.explained_variance_ratio_.cumsum())
Unfortunately, it looks like PCA would only be able to remove a relatively small amount of dimensions while maintaining reasonable accuracy, so it doesn't look like it will be able to help too much.
So how do we reduce the dimensionality of this?
The answer is relatively simple: we can simply remove our one hot encoded types, since we now express our types through weaknesses and resistances rather than the types themselves. This drops our dimensionalitiy from 28 to 10.
Let's see how this affects accuracy:
new_types_toadd = ['resistances', 'weaknesses', 'stab_sups', 'stab_nves']
keys = stats_toadd + ['fully_evolved'] + new_types_toadd
results = test_clf(keys, pokemon, "tier_numeric_coarse")
print(np.mean(results))
As you can see, our accuracy actually increased after we removed the one hot encoded types. This is because our reduced dimensionality allows the classifier to learn more effectively, resulting in increased accuracy. Additionally, we've improved our accuracy from our original by roughly 3%.
Abilities¶
Similar to how we originally added typing, abilities are also encoded ordinally. Similar to typing, we can't perform one hot encoding effectively due to the high cardinality of abilities.
Unfortunately, since abilities are relatively complex, we also can't quantify it as easily as we did with type effectiveness. However, abilities are crucial in determining a Pokemon's viability, so what do we do?
As far as I know, there isn't really an objective way to do this. What we can do, however, is "rank" abilities based on how strong they are. This is unfortunately subjective, but it is, generally speaking, fairly obvious if an ability is strong or weak.
So, we tier the abilities as follows:
- 0: crippling, ruins the Pokemon (e.g. truant)
- 1: no effect or weak (e.g. run away)
- 2: decent (e.g. shed skin)
- 3: strong (e.g. levitate)
- 4: game-changingly strong (e.g. wonder guard)
ability_tier = {
"Cacophony": 1,
"Stench": 1,
"Drizzle": 4,
"Speed Boost": 4,
"Battle Armor": 1,
"Sturdy": 1,
"Damp": 1,
"Limber": 1,
"Sand Veil": 1,
"Static": 1,
"Volt Absorb": 3,
"Water Absorb": 3,
"Oblivious": 1,
"Cloud Nine": 1,
"Compound Eyes": 1,
"Insomnia": 1,
"Color Change": 1,
"Immunity": 1,
"Flash Fire": 3,
"Shield Dust": 1,
"Own Tempo": 1,
"Suction Cups": 1,
"Intimidate": 3,
"Shadow Tag": 4,
"Rough Skin": 1,
"Wonder Guard": 4,
"Levitate": 3,
"Effect Spore": 1,
"Synchronize": 1,
"Clear Body": 2,
"Natural Cure": 2,
"Lightning Rod": 3,
"Serene Grace": 2,
"Swift Swim": 3,
"Chlorophyll": 2,
"Illuminate": 1,
"Trace": 2,
"Huge Power": 4,
"Poison Point": 1,
"Inner Focus": 1,
"Magma Armor": 1,
"Water Veil": 1,
"Magnet Pull": 2,
"Soundproof": 1,
"Rain Dish": 1,
"Sand Stream": 4,
"Pressure": 1,
"Thick Fat": 3,
"Early Bird": 1,
"Flame Body": 1,
"Run Away": 1,
"Keen Eye": 1,
"Hyper Cutter": 1,
"Pickup": 1,
"Truant": 0,
"Hustle": 2,
"Cute Charm": 1,
"Plus": 1,
"Minus": 1,
"Forecast": 2,
"Sticky Hold": 1,
"Shed Skin": 2,
"Guts": 2,
"Marvel Scale": 2,
"Liquid Ooze": 1,
"Overgrow": 1,
"Blaze": 1,
"Torrent": 1,
"Swarm": 1,
"Rock Head": 1,
"Drought": 3,
"Arena Trap": 4,
"Vital Spirit": 1,
"White Smoke": 2,
"Pure Power": 4,
"Shell Armor": 1,
"Air Lock": 2,
"Tangled Feet": 1,
"Motor Drive": 3,
"Rivalry": 1,
"Steadfast": 1,
"Snow Cloak": 1,
"Gluttony": 2,
"Anger Point": 1,
"Unburden": 2,
"Heatproof": 3,
"Simple": 2,
"Dry Skin": 3,
"Download": 2,
"Iron Fist": 2,
"Poison Heal": 3,
"Adaptability": 3,
"Skill Link": 3,
"Hydration": 1,
"Solar Power": 1,
"Quick Feet": 1,
"Normalize": 1,
"Sniper": 1,
"Magic Guard": 3,
"No Guard": 1,
"Stall": 0,
"Technician": 3,
"Leaf Guard": 1,
"Klutz": 1,
"Mold Breaker": 1,
"Super Luck": 1,
"Aftermath": 1,
"Anticipation": 1,
"Forewarn": 1,
"Unaware": 3,
"Tinted Lens": 1,
"Filter": 2,
"Slow Start": 0,
"Scrappy": 2,
"Storm Drain": 3,
"Ice Body": 1,
"Solid Rock": 2,
"Snow Warning": 2,
"Honey Gather": 1,
"Frisk": 1,
"Reckless": 2,
"Multitype": 2,
"Flower Gift": 1,
"Bad Dreams": 1,
"Pickpocket": 1,
"Sheer Force": 3,
"Contrary": 2,
"Unnerve": 1,
"Defiant": 2,
"Defeatist": 0,
"Cursed Body": 1,
"Healer": 1,
"Friend Guard": 1,
"Weak Armor": 1,
"Heavy Metal": 1,
"Light Metal": 1,
"Multiscale": 3,
"Toxic Boost": 2,
"Flare Boost": 2,
"Harvest": 2,
"Telepathy": 1,
"Moody": 1,
"Overcoat": 1,
"Poison Touch": 1,
"Regenerator": 3,
"Big Pecks": 1,
"Sand Rush": 3,
"Wonder Skin": 1,
"Analytic": 1,
"Illusion": 1,
"Imposter": 3,
"Infiltrator": 1,
"Mummy": 1,
"Moxie": 3,
"Justified": 2,
"Rattled": 1,
"Magic Bounce": 3,
"Sap Sipper": 3,
"Prankster": 4,
"Sand Force": 2,
"Iron Barbs": 2,
"Zen Mode": 1,
"Victory Star": 1,
"Turboblaze": 1,
"Teravolt": 1,
"Aroma Veil": 1,
"Flower Veil": 1,
"Cheek Pouch": 1,
"Protean": 3,
"Fur Coat": 3,
"Magician": 1,
"Bulletproof": 1,
"Competitive": 2,
"Strong Jaw": 2,
"Refrigerate": 3,
"Sweet Veil": 1,
"Stance Change": 3,
"Gale Wings": 2,
"Mega Launcher": 2,
"Grass Pelt": 1,
"Symbiosis": 1,
"Tough Claws": 3,
"Pixilate": 3,
"Gooey": 1,
"Aerilate": 3,
"Parental Bond": 4,
"Dark Aura": 2,
"Fairy Aura": 2,
"Aura Break": 2,
"Primordial Sea": 4,
"Desolate Land": 4,
"Delta Stream": 4,
"Stamina": 1,
"Wimp Out": 1,
"Emergency Exit": 1,
"Water Compaction": 2,
"Merciless": 1,
"Shields Down": 1,
"Stakeout": 1,
"Water Bubble": 3,
"Steelworker": 2,
"Berserk": 2,
"Slush Rush": 2,
"Long Reach": 1,
"Liquid Voice": 1,
"Triage": 2,
"Galvanize": 3,
"Surge Surfer": 2,
"Schooling": 1,
"Disguise": 4,
"Battle Bond": 3,
"Power Construct": 4,
"Corrosion": 1,
"Comatose": 1,
"Queenly Majesty": 2,
"Innards Out": 1,
"Dancer": 1,
"Battery": 1,
"Fluffy": 3,
"Dazzling": 2,
"Soul-Heart": 2,
"Tangling Hair": 1,
"Receiver": 1,
"Power of Alchemy": 1,
"Beast Boost": 3,
"RKS System": 1,
"Electric Surge": 3,
"Psychic Surge": 3,
"Misty Surge": 3,
"Grassy Surge": 3,
"Full Metal Body": 2,
"Shadow Shield": 3,
"Prism Armor": 2,
"Neuroforce": 2,
}
for p in pokemon:
p['ability_tier'] = max([ability_tier[x] for x in p['abilities']])
Now that we've tiered the abilities, let's see if it results in any improvement:
ability_col = ['ability_tier']
toadd = stats_toadd + new_types_toadd + ability_col + ["fully_evolved"]
results = test_clf(toadd, pokemon, "tier_numeric_coarse")
print(np.mean(results))
Okay, so adding abilities doesn't really improve our accuracy much - we have under a 1% increase. Why does this happen when ability plays such a crucial role?
In my opinion, this is because Pokemon with good abilities tend to be strong even without those abilities. For example, Primal Groudon has insane stats as well as a very strong ability. While there are indeed Pokemon whose viability is determined almost solely through their ability (such as Dugtrio with Arena Trap or Slaking with Truant), the amount of Pokemon like this is small relative to the Pokemon who are strong even without their strong ability. Furthermore, even a broken ability (Wonder Guard) sometimes can't carry a Pokemon such as Shedinja, with a cripplingly low 1 HP stat.
In addition, the "rank" an ability gets is subjective, and is not necessarily perfectly accurate.
This means that the ability generally isn't a super strong indicator of tier, despite ability being important when determining viability. As a result, we get only a small accuracy boost by quantifying Pokemon abilities.
However, a small boost is still better than no boost, so I'm counting that as a win on our part.
Movepool¶
So... the big one here is movepool. As mentioned before, a Pokemon's movepool matters a lot when determining a Pokemon's competitive viability. If a Pokemon only knew splash (which does nothing), for example, they could have 200 in each stat and it would still suck.
Unfortunately, our current data doesn't actually have movepools in our data, so we'd need to obtain the data somewhere else. Smogon indeed has data on the movepools of each Pokemon, but as far as I could tell, this was only visible on the page designated for each Pokemon. We would have to scrape every page separately, resulting in around 1000 requests, which probably isn't the best idea.
There's also the problem of how to actually use the movepool. As we've seen with abilities, subjectively rating movepools likely won't be very effective. Furthermore, movepools are even more complex than abilities! I was unable to think of a good way to incorporate movepools into our data, and as a result will leave it as an exercise to the reader (ha!).
Classifier model¶
That's pretty much it in terms of what sort of new data we can add that would make a significant impact on our classifier. But, if you recall the figure from scikit-learn that I posted, there are actually multiple models we can try. Perhaps one of the other ones (that aren't Linear SVC) will give us better accuracy? Let's find out.
def test_clf_knn(toadd, pokemon, ycol):
X = to_df(toadd, pokemon)
y = np.array([p[ycol] for p in pokemon])
classifier = KNeighborsClassifier()
scores = cross_val_score(classifier, X, y, cv=10)
return scores
def test_clf_svc(toadd, pokemon, ycol):
X = to_df(toadd, pokemon)
y = np.array([p[ycol] for p in pokemon])
classifier = svm.SVC()
scores = cross_val_score(classifier, X, y, cv=10)
return scores
def test_clf_rf(toadd, pokemon, ycol):
X = to_df(toadd, pokemon)
y = np.array([p[ycol] for p in pokemon])
classifier = RandomForestClassifier()
scores = cross_val_score(classifier, X, y, cv=10)
return scores
def test_clf_nb(toadd, pokemon, ycol):
X = to_df(toadd, pokemon)
y = np.array([p[ycol] for p in pokemon])
classifier = GaussianNB()
scores = cross_val_score(classifier, X, y, cv=10)
return scores
def test_clf_bag(toadd, pokemon, ycol):
X = to_df(toadd, pokemon)
y = np.array([p[ycol] for p in pokemon])
classifier = BaggingClassifier(KNeighborsClassifier())
scores = cross_val_score(classifier, X, y, cv=10)
return scores
ability_col = ['ability_tier']
toadd = stats_toadd + new_types_toadd + ability_col + ['fully_evolved']
results = test_clf_knn(toadd, pokemon, "tier_numeric_coarse")
print(np.mean(results))
results = test_clf_svc(toadd, pokemon, "tier_numeric_coarse")
print(np.mean(results))
results = test_clf_rf(toadd, pokemon, "tier_numeric_coarse")
print(np.mean(results))
results = test_clf_nb(toadd, pokemon, "tier_numeric_coarse")
print(np.mean(results))
results = test_clf_bag(toadd, pokemon, "tier_numeric_coarse")
print(np.mean(results))
Unfortunately, none of these classifiers perform much better - only SVC performs better than linear SVC, and by less than 1%.
Part 5: Results¶
And so, we've trained a classifier here to determine a Pokemon's competitive viability. We incorporated a Pokemon's typing, it's stats, and its movepool to achieve just under 90% accuracy. 90% isn't particularly high, but considering our dataset is relatively small at less than 1000 entries, and doesn't really have much redundancy (as Pokemon are designed specifically to be unique), I'd say that 90% is pretty okay.
If one were to try to improve this, the most obvious thing to do would be to incorporate a Pokemon's learnset into the classifier somehow.
Another major component that I haven't really touched upon is how Pokemon are affected by other Pokemon in the meta. If there are a lot of strong water types, for example, fire type Pokemon will be weaker than they would be otherwise. There's probably more nuanced stuff that I'm missing (as I'm not very good at competitive Pokemon in the first place). Point is, there's a lot of ways to potentially improve this classifier. If you're feeling up to it, feel free to build off anything you've seen here!
Anyways, I hope you've learned something by reading all this!